1.光辐射的量子假设
爱因斯坦在早期曾致力于热辐射的研究。从1901年开始,他在德国物理学杂志上发表了数篇关于热力学与统计物理的论文。从这些研究成果中,不仅看出他在统计物理方法运用上的熟练与精湛,更能看出他洞察潜藏在具体事件背后的基本性与普遍性问题上的惊人能力。在1905年他发表的重要论文《关于光的产生与转化的一个启发性观点》①中,他指出了麦克斯韦电磁理论的主要缺陷在于,这是一个关于“连续空间函数”的理论,它仅对时间平均值的光学观测有效。当把这一“用连续空间函数进行运算的理论用到光的产生与转化现象上时,这个理论会导致与经验相矛盾。”在批评麦克斯韦电磁学理论不足的同时,他还尖锐地揭示了普朗克量子论的不彻底性。他认为,该理论在考虑了黑体空腔器壁上的谐振子量子化的同时,却把腔内辐射场当作连续分布的麦克斯韦电磁场。他指出,即使普朗克量子论在黑体辐射上取得了成功,却不能对光电效应做出解释。从这两种理论的缺陷中,爱因斯坦找到了出路,这就是摒弃麦克斯韦的连续场,大胆地提出光量子的假设,“在我看来,如果假定光的能量不是连续分布在空间,那么,我们就可以更好地解释黑体辐射、光致发射、紫外线的产生、阴极射线及其它涉及光的发射与转换现象的各种观测结果。”他更进一步指出,能量“是由一个数目有限的局限于空间的能量子组成,它们在运动中并不瓦解,并只能整个地吸收或发射”,这就是爱因斯坦的光量子。1926年,美国化学家路易斯(Lewis, Gilbert Newton1875~1946)又将光量子定名为光子。爱因斯坦在他的同一篇论文中,又采用了维恩的辐射定律,从计算得出黑体辐射熵差公式与理想气体熵差两公式的相似性,由此得出光是由大小为Rβv/N的能量子组成的结论。接着,他利用光量子的假设,对斯托克斯光致发射定则、光电效应和紫外线对气体电离作用结果,做出了圆满的解释,所导出的著名的光电效应方程又为实验验证提供了准确的途径。爱因斯坦的这篇著名论文,成为了辐射量子研究的开端。爱因斯坦的光量子假设在物理界得到了热烈的反响。光能量量子化的思想特别得到了发现电荷量子化的美国物理学家密立根(Millikan. Robert Anderews1868~1953)的共鸣。密立根首先对爱因斯坦光电效应方程给出了实验验证。1914~1916年,在所发表的三篇论文中①,密立根叙述了他多年来进行的精心实验结果。它们不仅证实了爱因斯坦光量子的预言,还测出了普朗克常量,所得结果与普朗克本人用其它方法得到的数值极为相近。1915年,杜安(W.Duane)与他的同事,又从另一角度给出了爱因斯坦光电效应方程的证明①。他们利用能量已知的电子轰击金属靶,得到了X射线辐射,其频率可由公式1/2mv2=hv精确地给出。这是爱因斯坦方程的一种逆形式。后来,韦伯斯特(D.L.Webster)实验确定了上述频率的X射线标识谱的激发电位,给出了吸收限频率的v值②。正是由于对爱因斯坦方程逆形式的研究,使玻尔发现,电子的碰撞并不是把任意大小的能量传递给原子,而只能传递原子两态间的能量之差。这项研究导致了谱线吸收与发射的理论研究进展。1921年,德布罗意与艾利斯(C.D.Ellis)分别精确地测定了从不同能级上发射的电子的速度,在高频范围内,出色地给出了爱因斯坦方程更为直接的证明③④。1916年,爱因斯坦又在题为《关于辐射的量子理论》一文⑤中,提出了光子的动量概念。他认为“几乎所有的热辐射理论都有赖于辐射与分子间相互作用的考察”,在这种相互作用中,“尽管辐射给予的冲量很小”,“可是对于理论研究来说,却应该把那个小的作用和辐射所引起的明显的能量转移完全等同地看待。”他还指出“因为能量与冲量总是紧密联系在一起的,因此,只有证明了根据这个理论所得到的辐射传递给物体的冲量所引起的运动,正好是热学理论所要求的那样,这个理论才可以认为是完备的。”
尽管爱因斯坦的光量子假设在对光的发射与吸收、光电效应、固体的比热与温度的关系、紫外线对气体的电离作用等一系列光参与的动量与能量交换与传递的现象给出了圆满的解释,但是,光量子概念直到1923年,康普顿效应被发现后,才被物理界普遍接受与运用。
1912年劳厄在弗里德里奇及尼克平的协助下所完成的X射线晶体衍射实验,证实了X射线是一种波长很短的电磁波。根据麦克斯韦电磁理论,应能较好地解释这种波与带电粒子相互作用的情况,然而事实上却产生了困难。首先,根据电磁波理论,波的交变电场应能引起散射体电子做受迫振荡,振荡频率应当与入射线的频率相同,所以散射的频率也应与入射线的频率一致;其次,散射强度的分布应当相对电子的运动直线对称,且与辐射方向与电子运动方向夹角的正弦成正比。实验中却发现了不同的情况,从1912~1920年间,人们陆续地发现,对于波长很短的X射线或γ射线,沿入射方向向前的辐射强度大于向后的辐射强度,而且散射光的频率与入射线的频率不同,波长的改变量与入射线波长无关,只由散射角决定。1922年,康普顿把来自钼靶的单色化的X射线投射到石墨上,借助布喇格晶体光谱仪精确地测量了不同方向上的散射X射线的强度与波长。发现,散射光中既包含有原入射线波长的成分,又包含有比原入射线波长大的成分,这一现象称为康普顿效应。
康普顿效应无法用经典电磁理论解释。1923年,康普顿利用光量子假设对实验做出了成功的分析。他认为所谓X射线散射,实际上是光子与静止电子的弹性碰撞,散射效应中出现波长增大的波,是由于散射波的能量比入射辐射的能量小,所损失的能量是在碰撞中光子把一部分能量传递给电子所致。康普顿根据粒子碰撞的动量与能量守恒关系,导出了波长改变量与散射角的关系,这一结果恰好与实验观察一致。
康普顿效应证实了X射线的量子性,为爱因斯坦的光子假设的正确性提供了一个确凿的证据,它证明了光子不仅具有能量还具有动量,光子也与电子和其它微观粒子一样,遵守着能量与动量的守恒。除此以外,康普顿在得到散射公式时,还大胆地采用了当时并未被普遍接受的相对论理论。他认为,由于相撞粒子的速度很大,对它们的能量与冲量需用相对论公式。这一解释的成功,也是狭义相对论的最早也最出色的应用。因此,康普顿效应在近代物理学的发展中占有重要作用。康普顿为此获得1927年诺贝尔物理奖,当时他年仅35岁。
2.波粒二象性与德布罗意的位相和谐定律
1909年,爱因斯坦在《论辐射问题的现状》一文中①,利用普朗克辐射公式讨论了热平衡系统的能量涨落。所得到的公式是
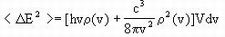
式中E2为频率为v的辐射能量,ρ(v)为频谱函数。爱因斯坦发现,当采用维恩观点,即把辐射当作由微粒组成的理想气体时,代入维恩的频谱函数,由公式得出的能量涨落将只有上式中的第一项;而当采用相反的观点,即认为辐射场能量在各个经典自由度上均分,而使用瑞利-金斯公式时,则只得到上式中的后一项。这表明,公式中的两项分别反映了各自独立的两种涨落机制。爱因斯坦意识到,用单一的观点或理论,不能完整地说明光的行为。在对两种理论的权衡对比中,爱因斯坦萌发了二象性这一重要思想。爱因斯坦认为,光的波粒二象性,不仅对于辐射理论,对整个物理学的研究也具有重要意义,它的作用是带有普遍性与根本性的。在1909年9月德国自然科学大会第81次会议上,爱因斯坦以《论我们关于辐射的本质与组成的观点》为题作了演讲。他指出“理论物理发展的下一阶段将给我们带来一种可以认为是波动论和发射论相结合的理论……我们对光的本性和结构的观点的深刻改革已是不可避免的。”
正如爱因斯坦所预见,波粒二象性概念给物理学带来的影响是极其深远的。1924年7月,印度物理学家玻色(Bose,Satyendranath 1894~1974)将题为《普朗克准则和光量子假设》的一篇论文寄给爱因斯坦征求意见。爱因斯坦将它译成德文,并加注给予了高度的评价,将其推荐发表在德文物理学期刊上。玻色的这篇论文采用了计入光子系统所有可能的各种微观状态和统计方法,导出了黑体辐射公式,证明了普朗克公式可以由爱因斯坦的量子气模型导出。同一年,爱因斯坦把玻色的统计方法加以推广到静止质量不为零、粒子数不变的系统上,提出了一种用于亚原子粒子的量子统计方法,这就是量子统计中著名的玻色-爱因斯坦统计。以后,狄喇克又把服从玻色-爱因斯坦统计的粒子,称为玻色子。爱因斯坦与玻色的这一出色工作,对后来的费密统计的建立起了很大的推动作用。在对光量子二象性的研究同时,类似的研究也在同期地进行着,这就是对实物粒子的二象性研究。1913年,玻尔提出了原子结构的量子理论,该理论给出了电子沿定态轨道的运动能量及辐射的频率公式。对于这一成功,法国物理学家布里渊(Brillouin,MarcelLouis1854~1948)却有着另一番解释。从1919~1922年间,布里渊发表了一系列论文,对玻尔量子化条件提出了理论解释。他认为,电子沿不连续的定态轨道运动,以及原子体系以不连续方式辐射能量,都反映了一种周期性。这种周期性应当可以从经典力学出发,用相干驻波的途径加以解释。他假定,形成波的介质是以太,在原子核的四周有一个以太层,电子在其中运动,使以太受到扰动而形成以太波,这些波相互干涉。若电子的运动稳定,相干结果,以环状驻波形式固定下来。玻尔用来标记定态的整数,正是这种排列在圆轨道上的波的数目。就这样,布里渊给神密莫测的玻尔正整数定态标记一种物理图象。然而,当把这一图象进一步推广时,却遇到了难以克服的困难,因而在这一思想的基础上,并没有建立起一个完整的理论来。尽管如此,布里渊的思想却起到了不可忽视的作用。布里渊曾把自己关于原子的核模型的工作结果寄给了法国物理学家德布罗意(DeBroglie,LouisVictorPierreRaymond,Prince1892~1960)。与布里渊一样,德布罗意也对玻尔模型中一系列整数标记的引入产生了兴趣。比布里渊更进一步,他更透彻地想到了其中必有更普遍与更本质的东西。他认为,“为了标志定态而诉诸整数的作法,似乎指明了研究的方向,整数,似乎只有在必须诉诸波动的那些物理学分支,如弹性学、声学和光学中出现。”最初,德布罗意认真地研究了布里渊的工作,布里渊假定电子在以太层中运动引起了以太层的波动,这实质上是一种介质波。德布罗意认为,出现困难的症结即在于引进了介质波。以后的进展表明,德布罗意不仅摒弃了以太概念,还把本属于电子的周期运动还给了电子自身,并始终如一地坚持了他的波动性与粒子性相结合的思想。
德布罗意的波动性与粒子性相结合的信念,从一开始,就在他1924年的博士论文之中表现了出来。这篇论文以《量子论研究》为题,提出了位相和谐定律与缔合波的思想,这是论文的核心与出发点。位相和谐定律表明,“对任意的伽利略观察者,粒子的固有时钟位相等于它的缔合波位相”。从这一原理出发,德布罗意得到了两个著名的公式,E=hv,λp=h,λ与v分别表示波长与频率,E与p分别表示能量与动量。这一结果揭示,一切具有动量与能量的物质客体,如电子等,也同时具有波动性。在光的波粒二象性尚未被完全地普遍接受时,在一部分著名物理学家仍为其感到困扰时,年轻的德布罗意却由此得到启发,大胆地把它推广到物质客体上,这不能不称为是一个伟大的思想。1972年,法国科学院庆祝了德布罗意80岁诞辰。在这一庆祝会上,德布罗意在致答词中,引用了著名哲学家柏格森(Bergson,Henri1859~1941)1927年获诺贝尔奖演讲中的一句话:“一个人在其一生中只能有一个伟大思想”,他说,“如果我确实有过这么一个思想的话,它无疑就是我在1924年写的博士论文第一章所表述出来的位相和谐定律。”①据德布罗意的学生罗切克(GeorgesLochak)回忆②③德布罗意并不认为波粒二象性是他的最大贡献,相反,他对玻尔常提到的波粒二象性还颇为反感。玻尔的波粒二象性与德布罗意的位相和谐思想不同,玻尔相信存在两面性的实在,然而这两面性是分别独立出现的,即在某种情况下表现出粒子性,在另一种情况下表现出波动性。而德布罗意却坚信,始终是一种东西,同时既是波又是粒子,这就是波与粒子的缔合,这种缔合反映在波频与粒子内部周期运动频率的合谐,描述波的线性方程的位相必须与描述粒子的非线性方程的位相相协调,粒子局域于物质波之中。
德布罗意的这一伟大思想对物理学的发展产生了深远的影响。 1926年,薛定谔(1887~1961)在发表他的波动力学论文时,曾明确表示:“这些考虑的灵感,主要归因于德布罗意先生独创性的论文。”电子的波动性很快地被证实,1927年,美国的戴维孙(Davisson,ClintonJoseph1881~1958)、革末(Germer,LesterHelbert1896~1971)及英国物理学家汤姆孙(Thomson,SirGeogePaget1892~1975)分别实验证实了电子的波动性。德布罗意的理论被普遍接受,从而使他获得了1929年诺贝尔物理学奖。