简易的遗传算法及其在控制中应用

　　摘　要：鉴于一般智能控制理论的教科书对于遗传算法的介绍过于深奥难懂，特写此文，通俗介绍遗传算法，并且提出自己简易的变异算法和交叉算法，以及应用遗传算法的编程思路，以便工程人员应用和供同行专家评鉴。
　　关键词：寻优搜索；遗传算法；变异；交叉；应用

Easy genet algorithm and its applications to control syst

HUANG TuanHua,HU JianJun,LIU YaLi,CHEN MingLang

(Institute of Modern Physics,Chinese Academy of Sciences,Gansu L anzhou 730000 China)

　　Abstract：Owing to most of the textbooks of in telligent control theory introduce genetic algorithm too recondite to be underst ood,this easy genetic algorithm is presented.The easy mutation algorithm and cro ssover algorithm,as well as the programming thought trains of applications of ge netic algorithm are presented in order to be applied by engineers and judged by the experts in the fi.
　　Key words：optimal searching;genetic algorithm;mutation;crossove r;applications

0概述
　　上世纪60年代，密执根大学的一篇博士论文首次提及遗传算法。1975年John Holland正式创立遗传算法。1985年开始召开遗传算法的专门国际会议。此后遗传算法飞速发展、广泛应用。遗传算法与模糊数学、人工神经网络一起被称为“软计算”或者“智能计算”，给人以新方法、新思路。
　　大自然不断地给人类以启示。物种进化原理告诉我们：一个生物群体，通过杂交或变异，产生新个体，经过优胜劣汰的选择，使该群体不断优化，并且还会出现罕见的最优或次最优的 个体；这些其实都是由于基因的遗传与变异。遗传算法就是模仿生物遗传进化的机理而设计 出来的算法。遗传算法的设计不是为了研究生物遗传进化原理，而是为了解决某些实际的工 程技术问题。遗传算法是一种优化搜索算法，它提供了既有序又随机的寻优方法，尤其是对 解决复杂的优化问题特别有效。
　　现将几种寻优方法比较评述如下：
　　(1)解析法(如：牛顿法、龙格库塔法、梯度法等《数值计算》方法)方法成熟，有成套的软件工具；但要求被搜索的函数连续可导；它是单路线搜索，搜索结果与搜索起点有关，可能陷入局部极点。
　　(2)穷举法按照预先设定的试验点一一普查；但是试验点太多，工作量太大。
　　(3)优选法又叫“0.618法”(黄金分割法)，它可以大踏步地缩小试验区域。但是它只能应用在“单峰”(或“单谷”)而圆滑的试验域中。
　　(4)随机枚举法试验点的设定如“枚举法”一样，不过用伪随机函数rand()来产生要抽查的试验点，寻找最佳点。经过足够多的点抽查，如果某个最佳值长时间不被“突破”，那么 就把这点认作全局最佳点。当然，这是“碰机会”，其结果未必是“真正的”最佳点。
　　(5)遗传算法这是文中将要介绍的。它是多点同时搜索，把有序搜索与随机搜索结合起来；所以效率高，而且是全局寻优。
　　遗传算法广泛地应用于函数寻优、静态优化、优化调度、优化控制、专家系统、模式识别、图像处理、机器人、分子生物工程。它还可以与模糊技术、神经网络技术、自学习技术等结合使用，效果更佳。

1遗传算法
1.1设定
　　(1)基因：根据被优化的参数，设计每个个体的“基因”结点；为了方便，一般先把各参数编成数，然后依次把1－0信号安放在结点上；设个体基因结点数为m。(2)设一个群体有n个个体，而且为了编程计算方便，设每代的n不变；一般定n＝(2～3)m。(3)根据被寻优的问题，造出一个评判个体优劣的评价指标函数E；并用E(i)表示第i个个体的指标。(4)规定把指标最好的几个个体原封不动地保送到下一代(即复制)，把 指标最差的几个淘汰出局不得参与变异运算和交叉运算。关于进化(遗传)比率笔者建议：复制率0.1，淘汰率0.2，变异率0.4，交叉率0.5。为了便于编程而保持群体总数n世代不变，必须让复制率、变异率、交叉率之和为1。
1.2变异算法
　　在需要变异的数目中随机产生i，也可以按某种规则依次产生i；在结点数m内随机 产生m1,m2,…mj。从群体中取出第i个个体，让它的第m1，m2，…mj个基因结点作“1－0”跳变。
　　假设第i个个体的基因为：
　　
设只有m1＝5，称为“单基困变异”，则使第5个(设从左起数)基因“1－0”跳变，得到新个体是：
　　
设m1＝15、m2＝4、mj＝7，称为“多基因变异”，则使第15、4、7个(设从左起数)基因“1－0”跳变，得到新个体是：
　　
1.3交叉算法
　　在交叉运算之前，先两两配对。配对的方式，最好是随机配对；但是考虑到不重复的随机配对的编程困难，考虑到实际效果和便于编程，建议采用以下3种配对方式；如果需要交叉的个体是从第1号到第30号个体，那么第1种配对方式：1－2，3－4，…27－28，29－30；第2种方式：1－30，2－29，14－17，15－16；第3种：1－16，2－17，…14－29，15－30。在配对之后，在结点数m内随机产生m1，m2，…mj，然后进行基因交换。
　　例如，将要进行交叉的个体的基因以及与之配对的个体的基因为：
　　
设随机产生m1＝15、m2＝4、mj＝7，则将第m1、m2、mj个的基因交换，那么这2个新个体为：
　　
　　如果基因交换的规则改为，只随机产生一个m＝5，并且规定m以后基因全部交换，那么这2个新个体为：
　　
　　如果改规定m以前基因全部交换，那么这2个新个体为：
　　
　　如果改规定m以后7个基因交换，那么这2个新个体为：
　　
　　如果改规定m以前4个基因交换，那么这2个新个体为：
　　
　　总之，设计者可以灵活规定遗传算法。虽然从物种进化的自然事实而言，“变异”是极个别现象；但是从寻优搜索的角度来讲，交叉算法与变异算法是等价的。这里所介绍的遗传算法只是抛砖引玉而已，研究者还可以设计出其他方式的遗传算法和进化比率。总之，设计者在“多点同时优化搜索，把有序搜索与随机搜索结合起来”的原则下，可以自由地设计算法。

2应用于系统辨识
　　例如，设一阶线性系统的z传递函数G(z)＝
　
…，u(20)y(20)；求系数a,b,c。(系数精确度要求3%)
　　解：根据精确度要求，确定一个系数占用5 bits，3个系数为15 bits如下：
　　
　　所以每个个体的基因结点数为m＝15，于是把群体中个体数定为n＝3 0。
　　
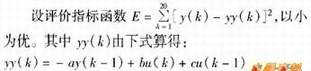
　　设复制率0.1，淘汰率0.2，变异率0.4，交叉率0.5。再设n表示个体数，i表示第几个个体；m表示基因数，j表示第几个基因；l表示第几代群体，k表示个体按评价指标E(i)大小排序。
　　编辑思路如下：
　　(1)给每个个体的系数数组赋以初值；
　　(2)计算每个个体的评价指标E(i)；
　　(3)根据评价指标排序，去掉最差的个体；
　　(4)根据变异算法产生新个体；
　　(5)根据交叉算法产生新个体；
　　(6)保留最佳个体，重复(2)～(5)操作，直至找到最佳系数数组。
　　这里介绍的是“离线辨识”。如果要编写“在线辨识”程序，以便插入自适应控制运行程序中去，那么请参考“在线递推辨识算法”和“自适应控制编程”的内容。这样就可以把遗传 算法应用于自适应控制系统。

3应用于控制系统

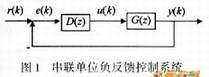
　　设控制系统如图1，已知预定值r(k)和被控对象G(z)，控制器D(z)的形式设计为：D(z)＝
　
就可以算出一系列y(k )、e(k)、u(k)。要求找出一组s0、s1、s2、r1、r2能够使得评价指标函数［e²(k)＋pu²(k)］最小，p是权因子。(系数精确度要求为0. 001)。
　　根据系数精确度要求确定每个系数要占用10 bits，5个系数共需要50 bits；就是 说m=50,于是n＝100。然后设定各进化比率和编程思路都和上述的类似。
　　由此可见，遗传算法是一种寻优方法。被寻优的参数是什么领域的，就叫做把遗传算法应用到什么领域；所以说，遗传算法可以广泛地应用于函数寻优、静态优化、优化调度、优化控制、专家系统、模式识别、图像处理、机器人、分子生物工程；同时，它还可以与模糊技术、神经网络技术、自学习技术等结合使用。

参考文献

［1］孙增圻.智能控制理论与技术［M］.北京：清华大学出版社，1997．
［2］王耀南.智能控制系统——模糊逻辑、专家系统、神经网络控制［M］.长沙：湖南大学出版社，1996．
［3］蔡自兴.智能控制——基础与应用［M］.北京：国防工业出版社，1998．
［4］John Yen,Reza Langari.Fuzzy Logic［M］.Preutice Hall,美国texas ,1998．
［5］S.G.Tzafestas.t.Computing in Systems and Control Techno logy［M］.美国：Robotics and Intelligent Systems Series,1997.